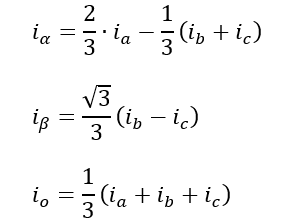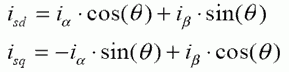Scalar Control
Scalar control (or V/Hz control) is a simple technique to control speed of induction motor.
The steady-state model of induction motor is mainly used to derive the technique, so transient performance is not possible. The system has no current loop. In order to control the motor the three-phase supply is varied only in magnitude and frequency.
Vector Control or Field Orientation Control
Torque in an electric motor varies as a function of the stator and rotor fields and is at its peak when the two fields are orthogonal to each other. In scalar based control the angle between the two fields varies considerably.
Vector control seeks to recreate the orthogonal relationship in the AC motor. To control the torque producing current separately from the magnetic flux producing current so as to achieve the responsiveness of a DC machine.
Vector control of an AC induction motor is analogous to the control of a separately excited DC motor. In a DC motor the field flux ΦF produced by the field current IF is perpendicular to the armature flux ΦA produced by the armature current IA. These fields are decoupled and stationary with respect to each other. Therefore when the armature current is controlled to control torque the field flux remains unaffected enabling a fast transient response.
Field Oriented Control (FOC) of a 3-phase AC motor involves imitating the DC motors' operation. All controlled variables are transformed to DC instead of AC via mathematical transformation. The goal is to control torque and flux independently.
There are two methods for Field Oriented Control (FOC):
- Direct FOC: Rotor flux angle is directly computed from flux estimation or measurement.
- Indirect FOC: Rotor flux angle is indirectly computed from available speed and slip computation.
Vector Control requires knowledge of the rotor flux position and can be computed using advanced algorithms from knowledge of the terminal current and voltages using dynamic model of the AC induction motor. However from an implementation standpoint the need for computational resources is critical.
Different methods can be used to implement the vector control algorithm. Feed forward techniques, model estimators and adaptive control techniques can all be employed to enhance response and stability.
Vector Control of AC Motors: An in-depth look
At the core of vector control algorithm are two important mathematical transforms: Clarke Transform, Park Transforms and their inverse. Use of the Clarke and Park transforms bring the stator currents which can be controlled into the rotor domain. Doing this allows a motor control system to determine the voltages that should be supplied to the stator to maximize the torque under dynamically changing loads.
Clarke Transformation: The Clarke mathematical transform modifies a three phase system to a two co-ordinate system.
where Iα and Iβ are components of the orthogonal reference plane and Io is the homoplanar component which is of little significance
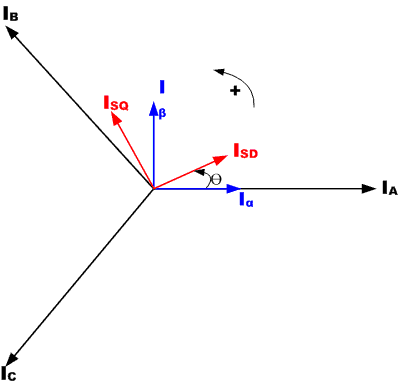
Park Transformation: The Park mathematical transform converts two-phase stationary system vectors to rotating system vectors
The two phases α, β frame representation calculated with the Clarke transform is then fed to a vector rotation block where it is rotated over an angle θ to follow the d, q frame attached to the rotor flux. The rotation over an angle θ is done according to the above formulas.
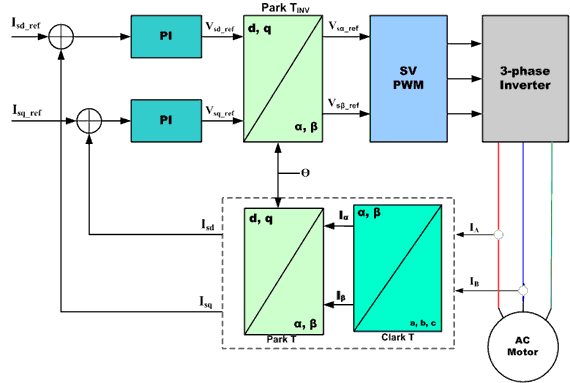
Basic Scheme for Field Oriented Vector Control of AC Motor:
Figure 2 shows the basic scheme for a Field Oriented Vector Control for an AC Motor.
The Clarke transform uses three-phase currents IA, IB and IC to calculate currents in the two-phase orthogonal stator axis: Iα and ;Iβ. These two currents in the fixed coordinate stator phase are transformed to the Isd and Isq currents components in the d, q frame with the Park transform. The currents Isd, Isq and the instantaneous flux angle θ, calculated by the motor flux model, are used to calculate the electric torque of an AC induction motor.
These derived values are compared against the reference and updated by a PI controller.
Comparison between Scalar and Vector Control for Motors
| Control Parameters | V/Hz Control | Vector Control | Sensorless Vector Control |
|---|---|---|---|
| Speed Regulation | 1% | 0.001% | 0.05% |
| Torque Regulation | Poor | +/- 2% | +/- 5% |
| Motor Model | Not Required | Required | Requires Accurate Model |
| MCU Processing Power | Low | High | High + DSP |
An inherent advantage of Vector based motor control is that the same scheme can be used to control various types of AC, PM-AC or BLDC motors by selecting the appropriate mathematical models for the respective motors.
Vector Control of BLDC Motors
BLDC motors are also prime candidates for Field Oriented Vector control. Brushless motors which adopt an FOC approach can achieve even higher efficiencies, up to 95 percent and are efficient at the very highest speed range of the motor.
| Control Methods | MCU Requirements | Suggested MCUs | ||||
|---|---|---|---|---|---|---|
| RL78 Family | RX Family | RH850 Family | RZ/T1 Group | |||
| AC Motor Control | V/F Control | Input Capture, Interrupt, PWM Timer for Three-Phase motor control | ● | |||
| Simplified Vector Control | Input Capture, Interrupt, PWM Timer with Deadtime for Three-Phase motor control | ● | ● | ● | ||
| Vector Control(FOC) | High Performance MCU + MAC, High-Speed A/D Converter, Input Capture, Interrupt, PWM Timer with Deadtime for Three-Phase motor control | ● | ● | ● | ||
| Sensorless Vector Control | High Performance MCU + MAC, High-Speed A/D Converter, Interrupt, PWM Timer with Deadtime for Three-Phase motor control | ● | ● | ● | ||