The specifications of semiconductor devices are usually prescribed based on an ambient temperature (TA: Air temperature around the device) or package surface temperature (TC) of 25 °C. Actual usage environments vary greatly, but in the case of characteristics or a tolerance range other than 25 °C, the user must perform calculations according to the usage environment for the device being designed using characteristics curves, etc.
General specification items are described below.
Absolute Maximum Ratings
Each item is basically specified for direct current. Therefore, if switching alternating current, think of the ratings on the output side as half-wave peak values (half of amplitude in the case of a sine wave).
Isolation Voltage: BV (Vrms)
The allowable maximum alternating current voltage that can be applied between the input pins and output pins is expressed as a root mean square (rms) value. This value guarantees a certain insulation resistance and is normally guaranteed not for an unlimited period, but for a limited test time, of 1 minute, for example.
Operating Ambient Temperature: TA (°C)
The allowable temperature range in which power application is possible. Usually when the actual ambient temperature rises, the power dissipation (PD) declines. Moreover, power application is inhibited when the actual ambient temperature is out of this range. In the case of OCMOS FETs, the temperature at which power can be applied is not described as the "package surface temperature", but instead as the "ambient temperature (air temperature around the device)".
Storage Temperature: Tstg (°C)
The allowable temperature range when power is not applied (stored state).
Light Emitting Diode: Forward Current: IF (mA)
The allowable maximum current at which destruction does not occur, within the allowable power dissipation (PD) range of the light emitting diode (LED) on the input side when the ambient temperature is 25 °C. In the case of OCMOS FETs, the forward current affects the response time, but has almost no influence on the static characteristics of output. However, since response time does not change so much and depends on the forward current larger than optimum value, excessively raising the forward current is not significant. Mainly with design circuits so that the maximum value of the forward current remains within this range, even if the forward current is subject to variations or fluctuations.
Light Emitting Diode: Reverse Voltage: VR (V)
Note that the reverse withstand voltage of the LED on the light-emitting side is low. When the reverse withstand voltage is exceeded, a reverse current suddenly flows. (In this case, the LED does not emit light.) Moreover, when a reverse current flows, the subsequent light emitting efficiency is lowered. Therefore, when a reverse voltage exceeding this value is applied even momentarily, destruction or non-recoverable degradation may occur.
Light Emitting Diode: Power Dissipation: PD (mW)
The allowable power dissipation of an LED on the input side at an ambient temperature of 25 °C. As described in the "Light Emitting Diode: Forward Current (IF)" section, in the case of OCMOS FETs, excessively raising the forward current is not significant.
MOSFET: Power Dissipation: PD (mW)
The allowable power dissipation of a MOSFET on the output side for an ambient temperature of 25 °C. In the case of OCMOS FETs, the output resistance is almost constant against the change of the load current in the "ON" state, so internal loss on the output side is almost obtained from the load current value.
MOSFET: Breakdown Voltage/Load Voltage: VL (V)
The allowable maximum voltage that can be applied between drains (and also between drain and source) when the MOSFETs on the output side are in the "OFF" state. If using the two MOSFETs on the output side with their opposite polarities connected in series, the half-wave peak values (half of amplitude in the case of sine wave) of the AC signal must not exceed this value.
MOSFET: Continuous Load Current: IL (mA)
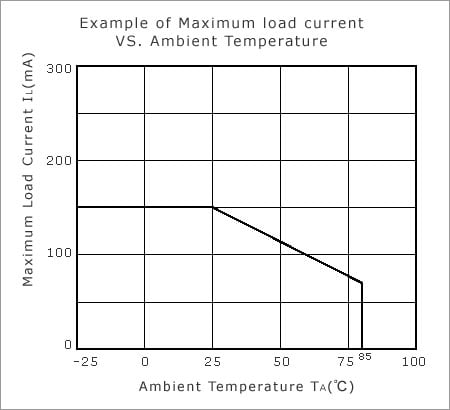
The allowable maximum value of the load current that can flow through the output MOSFET in the "ON" state. Whether DC or AC, keep the peak value (half of amplitude in the case of a sine wave) within this range. Because of the temperature dependency of allowable power dissipation, when the ambient temperature rises, this range declines as shown in the figure below.
MOSFET: Pulse Load Current: ILP (mA)
The allowable maximum DC load current that can flow through the output MOSFET for a prescribed short time only. This value is acceptable as long as it remains within the prescribed allowable range, including time limitations. Basically, cyclic application is not allowed.
Electrical Characteristics
Turn-on Time/Turn-off Time: ton, toff (ms)
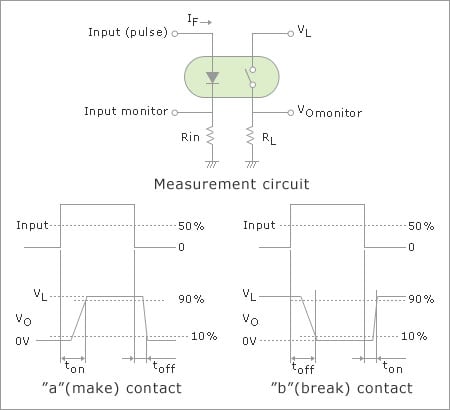
The delay time from the change of the forward current (IF) to the change of the output when a forward current flows through an LED on the input side as a pulse. In certain case, the shorter the input pulse width as stated in the datasheet, the longer the time (toff and ton as below mentioned) than either the value specified in the specification or the "Typical Characteristic" curve.
"a" (make) contact : turn-off time (toff)
"b" (break) contact : turn-on time (ton)
Please ensure that the input pulse width is operated within the specified range.
Isolation Resistance: RI-O (Ω)
The initial isolation resistance when a high direct-current voltage is applied between the input and output pins. Since the isolation resistance can decline depending on the usage environment, such as the humidity, or the application time of the voltage, perform design and testing while taking the actual usage conditions into consideration.
Isolation Capacitance: CI-O (pF)
The capacitance when a high-frequency signal is applied between the input and output pins. The larger this value, the more likelihood of noise getting output due to sudden fluctuations in the electric potential difference between input and output pins. Since this value may increase due to wiring conditions, etc., perform design and verification while taking these factors into consideration.
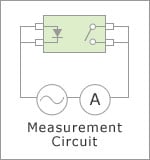
Light Emitting Diode: "ON" State Current: IFon (mA)
The minimum forward current (IF) required for turning-on the output of the "a" contact ("Make" contact: Normally open: Non-conducting when there is no input) type OCMOS FET. Input a forward current (IF) greater than this value, referring to the "turn-on time vs. forward current" curve and "turn-off time vs. forward current" curve, according to the required response time.
Light Emitting Diode: "OFF" State Current: IFoff (mA)
The minimum forward current (IF) required for cutting off the output of the "b" contact ("Break" contact: Normally closed: Conducting when there is no input) type OCMOS FET. Input a forward current (IF) greater than this value, referring to the "turn-on time vs. forward current" curve and "turn-off time vs. forward current" curve, according to the required response time.
Light Emitting Diode: Forward Voltage: VF (V)
This is the inter-pin voltage when a forward current flows through an LED on the input side. The product of this value and the forward current value expresses the internal loss of the input side. Generally, the increasing of the forward current or the falling of the ambient temperature causes rising of this voltage.
Light Emitting Diode: Reverse Current: IR (µA)
This current flows when a prescribed reverse voltage is applied within the maximum rating range to the LED on the input side. Generally, the increasing of the reverse voltage or the rising of the ambient temperature causes increasing of this current. In the case of circuits in which a reverse voltage is applied to the LED, design the drive circuit taking into consideration that this value is affected by usage conditions.
MOSFET: "OFF" State Leakage Current: ILoff (µA)
The drain leakage current when the MOSFET on the output side is non-conducting. Generally it is proportional to the signal voltage which is switched, and the rising of the ambient temperature causes this current to increase. Design the load resistor (or termination resistor) value taking into consideration that this current tends to be affected by the temperature.
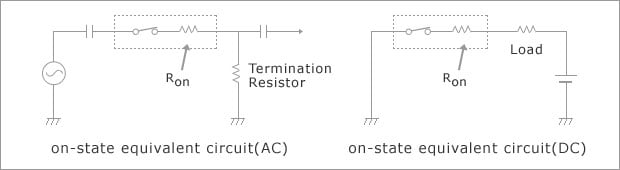
MOSFET: "ON" State Resistance: Ron (Ω)
Without otherwise specified, this is the resistance between drains when the MOSFETs on the output side are conducting. The load resistor (or termination resistor) value should be generally set to a value much greater than this value.
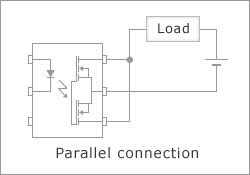
In the case of products which provide source pins, the "ON" state resistance between the drain and source of each MOSFET is approximately half of this rated value. Furthermore, by using of MOSFETs connected together in parallel as shown in the figure below, an "ON" state resistance approximately quarter of this rated value is expected (not guaranteed).
The "ON" state resistance is not influenced by the value of the forward current (IF) of the input side, but the rising of the ambient temperature causes this resistance to increase. Additionally, in the case of products of the high conduction resistance type, the "ON" state resistance tends to decline with the large load current, specifications are provided on both the small current area and the large current area. When using a large conduction resistance type product between the drain and source, apply the "ON" state resistance prescribed on the small current area.
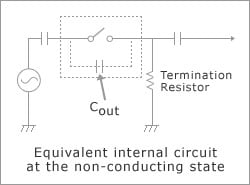
MOSFET: Output Capacitance: Cout (pF)
The capacitance between the output pins (between drain and drain) in relation to high-frequency signals, when the MOSFET on the output side is in the "OFF" state. The smaller the voltage between the output pins, the larger this value. Since AC signals leak through this capacitance in the "OFF" state, a fully "OFF" state cannot be obtained unless there is termination with a sufficiently small resistance for the higher frequency signal.